Handling Outlier in Data Analysis

I have to be frank; the only time I thoroughly understood the concept of outliers was when I read Malcolm Gladwell’s book: ‘Outliers’. Although I have come across the word in my undergraduate statistics class, the concept never sunk into my subconscious. I wasn’t lucky. My statistics lecturer taught statistics purely on a theoretical level with little or no connection with reality or real-life experience and application!
Gladwell borrowed the concept from the field of statistics and so with the help of ‘connection’ I gained a deeper understanding about one of the critical concept in statistics and by extension data science and machine learning! Today’s post shall therefore dwell on outliers, however, from the perspective of data preprocessing in data science and machine learning. To this end, we would cover:
- Meaning and definition of an outlier from data science and machine learning perspective
- The implication of outlier in our dataset if not treated
- Practical ways to detect and handle outliers
Outlier is a data point that differs significantly from other observations - Wikipedia
The above definition is quite apt and concise. From the angle of normal distribution and empirical rule, it is those data point which falls outside the three standard deviations of the mean. Care, however, should be observed to avoid assumption. Outliers are relatively amorphous; thus, we should tread carefully in an attempt to designate data points as outright outliers without rigorous investigation.
There is a situation where outliers play a critical function. Of course, this is dependent on the objective of the analysis, for example, where the study objective is to detect fraud in electricity usage. Under this scenario here, the concept of outlier would play a critical role. On the other hand, outlier could be an ‘experiment error’ in which case we should treat it accordingly else we risk erroneous interpretation and inference.
Identifying Outliers
Just as knowing or identifying a problem is the first step toward its solution. Similarly, to treat and handle outliers effectively, we must have the means of detecting it.
- Detecting outliers through constructing a box plot
- Through the IQR proximity rule
- Through Z score calculation
Since we try to be as practical as possible, we shall illustrate and demonstrate the above techniques with an example.
Under the IQR proximity rule, a value is an outlier if it falls outside these boundaries: upper_boundary = 75th quantile + (IQR *1.5) lower_boundary = 25th quantile - (IQR * 1.5)
Where IQR is calculated as IQR = 75TH quantile - 25th quantile However for an extreme case outlier we would multiply IQR by 3 instead of 1.5
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from sklearn.dataset import load_boston
from scipy.stats import zscore
Load the Boston House Prices dataset from scikit-learn and retain three of its variable in the data frame
bost_dataset = load_boston()
boston = pd.DataFrame(bost_dataset.data, columns=bost_dataset.feature_names)[['RM','LSTAT', 'CRIM']]
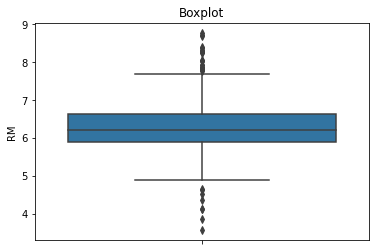
Make a boxplot for the RM variable
sns.boxplot(y=boston['RM'])
plt.title('Boxplot')
create a function that takes in a DataFrame the factor to use for the IQR and a variable name and returns the IQR proximity rule boundaries
def find_bound(df,var,distance):
IQR = df[var].quantile(0.75) - df[var].quantile(0.25)
lower_bound = df[var].quantile(0.25) - (IQR * distance)
upper_bound = df[var].quantile(0.75) * (IQR * distance)
return upper_bound, lower_bound
```
calculate and display the IQR proximity rule boundaries for *RM* variable
```python
upper_bound, lower_bound = find_bound(boston, 'RM', 1.5)
This returns the values above and below that are considered as outlier
We can create a boolian vector to flag observation outside the boundaaries we previously established
outliers = np.where(boston['RM'] > upper_bound, True, np.where(boston['RM'] < lower_bound, True, False))
We can equally create a dataframe with the outlier values and display the top five values
outlierdf = boston.loc[outliers, 'RM']
outlierdf.head()
Using zscore to detect outliers in RM variable
outlierz = zscore(boston['RM'])
# Decision: where the value +3 and above then it is an Outliers
The way and manner outliers are handled and treated would depend on the objective of the analysis or problem statement of the study. Overall when not handle appropriately, outlier could lead to erroneous inferences especially in the area of central tendency measurement as some of such measurement could be sensitive to inexplicably large values. Hope you learn something today. Bye!